Test Quiz 1

The content of the heavy metal Cadmium in canned tuna were measured in tuna from 3 different manufacturers of canned tuna. From each manufacturer 5 cans of tuna were randomly selected. The following quantities of Cadmium in $\mu$g$/$kg were measured in the 15 different cans of tuna:

Manufacturer 1:	57	52	62	49	43
Manufacturer 2:	55	74	62	42	52
Manufacturer 3:	61	54	55	53	51

What is the 3. quartile (upper) of the Cadmium content at Manufacturer 1? (Using the definition of the book)

52

54.5

57

The approach to calculate the third quartile is given in Chapter 1. First we have to order the measurements from smallest to largest: 43, 49, 52, 57, 62. Then we calculate $p \cdot n=0.75 \cdot 5=3.75$, and round it up to 4, and the third quartile is then measurement 4 which is 57. Note that in Python it would be solved as:


x = np.array([57, 52, 62, 49, 43])
np.quantile(x,[0,0.25,0.5,0.75,1],method='averaged_inverted_cdf')
array([43., 49., 52., 57., 62.])

52.6

55.75

A random sample of 10 estate agents showed that they had to show a property to 8, 7, 10, 14, 11, 7, 10, 11, 16, 12 different buyers before the property was sold.

The median for the number of showings of a property is? (using the definition of the book)

10.6

11

10.5

11.75

10

Boxplots for 3 different groups of data with $n=20$ data points in each group are shown below. (It can be assumed that there are no ‘‘ties’’, that is no identical observations.)

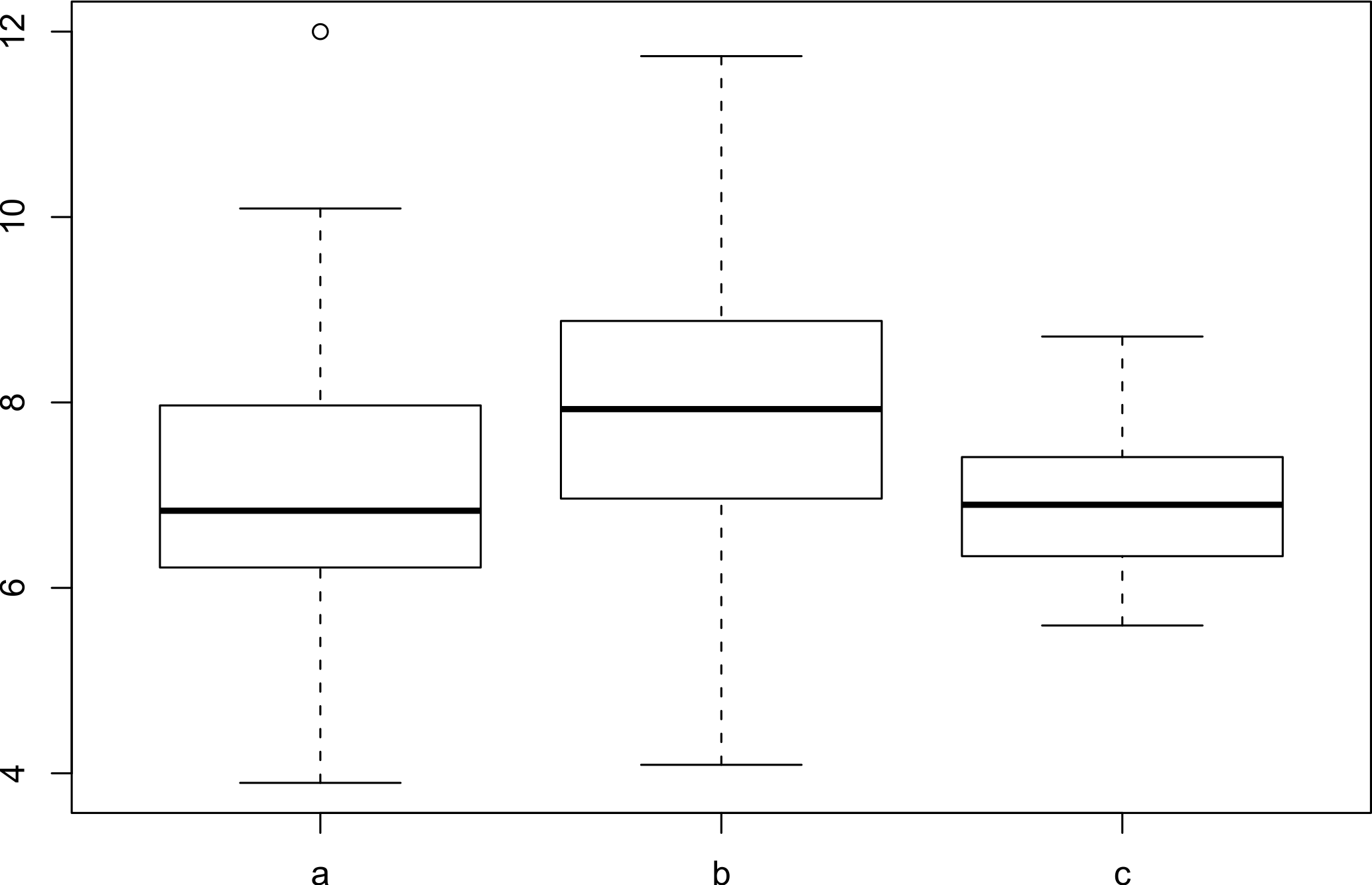
Boxplot

Which of the following statements is false?

The median for the data in b is approximately 8

The largest observation among all 3 groups of data is approximately 12

The data in boxplot c has the smallest variance

The 90th percentile for the data in boxplot a is approximately 12

The third quartile for boxplot c is approximately 7.4

In a redesigned valve the socalled “elasticity modulus’’ of the material is important for the functionality. To compare the elasticity modulus of 3 different brass alloys, samples from each alloy was purchased from 5 different manufacturers. The measurements in the table below indicates the measured elasticity modulus in GPa:

		Brass alloy		Row sum
	M1	M2	M3
Manufacturer A	82.5	90.9	75.6	249.0
Manufacturer B	83.7	99.2	78.1	261.0
Manufacturer C	80.9	101.4	87.3	269.6
Manufacturer D	95.2	104.2	92.2	291.6
Manufacturer E	80.8	104.1	83.8	268.7
Column sum	423.1	499.8	417.0

Consider only the data for brass alloy M1. The median and the upper quartile for these become: (using the book Chapter 1 definition)

Median = 82.5 and upper quartile=83.7

The ordered list of the $n=5$ numbers is: $80.8,80.9,82.5,83.7,95.2$. The middle number (median) is number 3 in this ordered list: $82.5$. The upper quartile is the 75\% percentile, and since $n\cdot 0.75=3.75$ this number is the 4th in the ordered list: $83.7$. hence the answer is:

Median = 82.5 and upper quartile=83.7 Had this been done in Python, we would get:


m1 = np.array([82.5,83.7,80.9,95.2,80.8])
np.quantile(m1, [0.5,0.75],method='averaged_inverted_cdf')
array([82.5, 83.7])

Median = 83.1 and upper quartile=89.45

Median = 84.62 and upper quartile=36.427

Median = 84.62 and upper quartile=95.2

Median = 82.5 and upper quartile=95.2

Two different brands of tablets with the same active compound are compared with respect to their solubility. For each of the two brands 10 tablets were investigated. For each tablet, percent solubility is measured after the tablet have been kept in 1000 ml de-ionized water for a while. One measurement failed, so the following values for $\%$ solubility were found:

Brand F	45	47	48	49	49	50	52	52	53	54
Brand G	48	48	49	49	52	54	54	55	55

What are the following five numbers for Brand G: $0\%$-percentile, lower quartile $Q_1$, median, upper quartile $Q_3$, and $100\%$-percentile?

$0$, $ 49.5$, $51.56$, $ 55$, $ 100$

$48$, $ 49$, $52$, $ 54$, $ 55$

With $n=9$ we could use the quantile definition procedure a number of times. However, since the median of these 9 numbers is the middle number, that is 52, the only possible correct answer is: $48$, $ 49$, $52$, $ 54$, $ 55$. (And we don’t have to think about how to define the 0\% and 100\% percentiles - which simply are defined as the minimum and maximum values) In Python:


brand_G = np.array([48, 48, 49, 49, 52, 54, 54, 55, 55])
   np.quantile(brand_G,[0,0.25,0.5,0.75,1],method = 'averaged_inverted_cdf')
   array([48., 49., 52., 54., 55.])

$0$, $ 25$, $50$, $ 75$, $ 100$

$51.56-2\cdot 3.05$, $ 51.56-3.05$, $51.56$, $ 51.56+3.05$, $51.56+2\cdot 3.05$

$51.56-2\cdot 3.05/9$, $ 51.56-3.05/9$, $51.56$, $ 51.56+3.05/9$, $51.56+2\cdot 3.05/9$

02402 · Test Quiz 1

Question 1 of 5

Question 2 of 5

Question 3 of 5

Question 4 of 5

Question 5 of 5